Market frictions or market failures are seen as one of the most common reasons, why economies in developing countries suffer from a lack of growth. Some stylized facts indicate a huge disparity in the productivity especially in the primary argricultural sector. The primary sector occupies a key place in the economy of developing countries. According to the UNDP in 1996 agriculture employed 60% of the labour force while contributing 20% of GDP of less developed countries, in comparison to 2% of the labour force contributing 2 % of GDP of developed countries. This indicates that there is a huge productivity gap across countries.

Assume a simple production technology and note that due to the concavity $$F(T)/T>F(T’)/T’$$ as long as $$T’ > T$$. Hence, average product is decreasing with a concave production function. This may explain the empirically observed inverse land-size productivity relationship, which has been observed e.g. by Berry & Cline, 1979 and many others to follow.

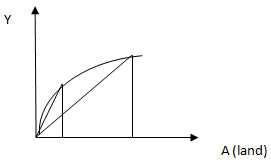
Graphically this is depicted in the simple picture

Here, as can be seen, average product is higher for small farms due to diminishing returns. Yet, with functioning markets, we should see an equalization going on. The productivity decisions should be independent of endowments as in functioning markets, the marginal returns should be equalized. In the absence of markets, e.g. due to a severe failure due to lack of property rights, markets may not exist.

So if these two farms are the only ones in the market, we should observe an equalization of average product across the two farms, i.e. the farm with the lower average product should rent out some land to the farmer with the higher average product.

One side note: Before Shaban (1987) the regressions that found the inverse landsize-productivity relationship the authors never controlled for individual heterogeneity, i.e. that some farmers may just be more productive, or controls for land quality were often not included. Shaban was among the first, to include this individual level data into the regressions to test on the presence of moral hazard in different types of sharecropping contracts.