I think I somewhat understood now finally theargument, how the speed of convergence in a simple Solow model is increased by access to world capital markets, if we are in a small, open-economy setup. Capital markets can be considered to be the “grease” for economies. They link savers to investors and create in a setup with risk-aversion a value-added due to their risk pooling abilities. In a simple Solow model, we can see how capital markets increase the speed of convergence.

Assume

$$y_t = k_t^{\alpha}$$

$$k_{t+1} = sy_t =s k_t^{\alpha}$$

so we have a simple Solow model with no depreciation.

The steady state is:

$$k^* = (s)^{\frac{1}{1-\alpha}}$$

$$y^* = (s)^{\frac{a}{1-\alpha}}$$

and finally, since $$r^* = f'(k^*) = \alpha (k^*)^{\alpha-1} = \frac{\alpha}{s}$$

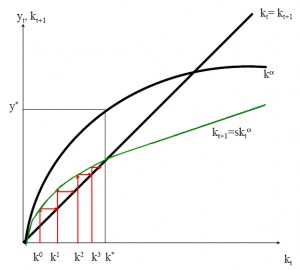
The process of convergence to the fixed point can be depicted in the folloing little graph. The green curve depicts the capital accumulation equation, the red arrows depict the convergence to the fixed point.

With competitive markets, it has to hold that the marginal value product of capital equals the interest rate, so:

$$r_t = f'(k_t) = \alpha A k_t^{\alpha-1}$$

Notice that this is indexed by time, i.e. the interest rate evolves as well. In a small open economy, the domestic interest rate has to equal the World interest rate $$r*$$, this is what will speed up convergence. If the economy is below its steady state, then the maginal returns to capital exceed the level of the world interest rate. This will induce capital to flow in and will immediately lead to convergence towards the steady state.

This will also imply that the GDP will be smaller than the GNP for some time.  This is because GDP is the market value of everything produced within a country; GNP is the value of what’s produced by a country’s residents, no matter where they live.

Due to the flow of capital from abroad into the domestic economy, GDP will immediately reach its steady state level $$y^*$$, yet the benefits from this income, i.e. the marginal returns due not entirely accrue to the domestic investors, but will partly flow to foreign investors.

This logic allows us to write the evolution of domestically owned capital as:

$$k_{t+1} = s (y^* -r^*(k^* – k_t))$$

Note that capital per-se will immediately jump to $$k^*$$. However, only part of this capital is owned by domestic investors.

If $$k_0$$ is the initial level of domestically owned capital, then one period later it is:

$$k_{1} = s (y^* -r^*(k^*-k_0))$$

This is out of the GDP per capita y^*, the proceeds of size $$r^*(k^*-k_0)$$ accrue to foreign investors; so domestically we are left with income per capita of size $$y^* -r^*(k^*-k_0)$$. Out of this, a constant amout is saved and invested in new domestic capital. So we see slowly, how foreign capital is driven out and we will observe an equalization of GNP and GDP in the long run.

But how do capital markets help here

One may be inclined to argue that access to capital markets do not help, as the capital income just accrues to the foreign capital owners and individuals still have to accumulate their own domestic capital out of “mere sweat”.

However, we can show that even with this, domestically owned capital grows faster with capital markets than without. Hence, there is still a positive effect.

To see this we compare the evolution of domestically owned capital in both cases. With access to capital markets we have:

$$k_{t+1} = s (y^* -r^*(k^* – k_t))$$

We can rewrite this using our Cobb-Douglas production function by substituting out $$y^*, r^* , k^*$$  from earlier we get:

$$k_{t+1} = (s)^{\frac{1}{1-\alpha}}(1-\alpha) + \alpha k_t$$

Compare this with the equation of motion in case we do not have capital markets:
$$k_{t+1} = s k_t^{\alpha}$$.

You can already see here, that the previous converges faster, as $$k_t$$ enters linearly, whereas it enters concave in the autarchy one. To see it even more formal, you can linearlize the non-linear autharchy equation of motion around the steady state. However, the essence is caputured in the following graph, where the yellow arrows indicate the faster convergence of domestically owned capital to the steady state value.

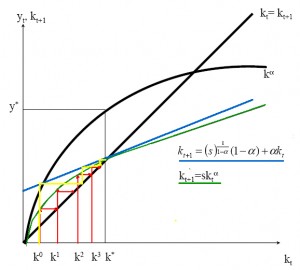
 So things to note: with capital markets, we will reach immediately the steady state level of GDP per capita. However, GNP will be smaller than GDP as some of the income accrues to foreign capital stock owners. In the long run, domestically owned capital stock converges to the steady state level. This occurs at a rate which is faster than if we do not have capital markets.

What is the intuition for this?

Essentially the reason is, that due to capital markets we move instantaneously to $$y^*$$, hence, also the factor labor receives a higher renumeration. So aggregate domestic savings are also higher and thus, total investment in domestic capital stock is period by period larger as compared to autarchy. This explains the faster speed of convergence.