Weak institutions and natural resource abundance are a recipe for civil conflict and the overexploitation of natural resources. Â In our forthcoming paper with the title “Take what you can: property rights, contestability and conflict”, Samuel Marden and I present evidence from Brazil indicating that insecure property rights are a major cause of land related conflict and a contributing factor in Amazon deforestation.
Brasil is a unique context. The contestability of property rights over land is enshrined into the Brazilian constitution. Land not in ‘productive use’ is vulnerable to invasion by squatters, who can develop the land and appeal to the government for title. This setup may cause violent conflict, between squatters and other groups claiming title to land. As such, weak property rights may distinctly affect conflict by directly and indirectly shaping the underlying incentives. Â
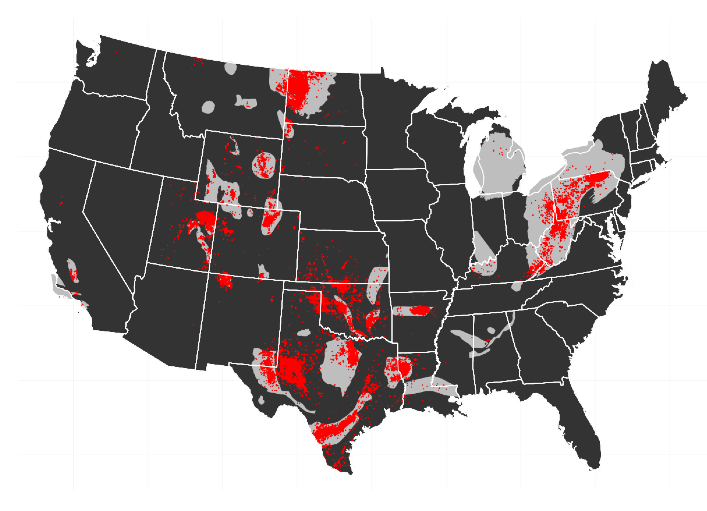
Protected Areas and Tribal Reserve Areas redefine the “productive use” of land, rendering the land not contestable anymore. We obtain variation in the share of municipal level that is contestable land by exploiting the dramatic expansion in the share of land under ecological or indigenous protection between 1997 and 2010.  An increase in the municipal share of land under protection reduces the share of land in that municipality that is contestable. 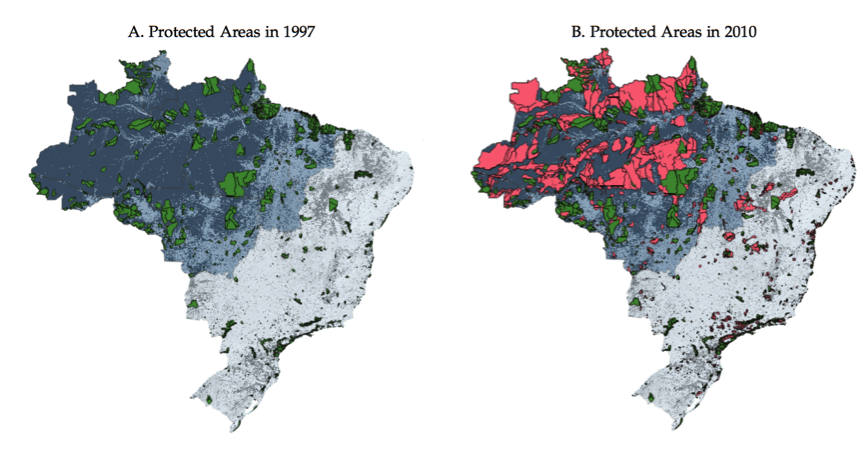 Property right assignment reduces land related conflict. Using this variation in the municipal share of land with contestable title in the Brazilian Amazon, we show that (in)secure property rights are strongly associated with land related conflict. We obtain these results using classical panel data regression methods, but also employ a novel quasi-event study approach.
Property right assignment reduces land related conflict. Using this variation in the municipal share of land with contestable title in the Brazilian Amazon, we show that (in)secure property rights are strongly associated with land related conflict. We obtain these results using classical panel data regression methods, but also employ a novel quasi-event study approach.
Effects on deforestation and land use change. Our empirical results on land conflict suggest that the creation of protected areas and indigenous areas, should have distinct effects on land use: since its not attractive to develop a land claim on protected land or land, where title has been given to indigenous groups, there should be limited incentives to invest in the land by deforestation.
There are two distinct channels:Â permanent deforestation of the type associated with cropland conversion should be dramatically reduced; temporary deforestation, such as due to illegal logging may actually increase if protection is not associated with significant increases in enforcement capacity.
Measuring deforestation and land use change. On the Amazon frontier, it is difficult to obtain reliable statistics about crop production or simple cattle ranching, as a lot of the farming is subsistence farming at small scale. Hence, official agricultural statistics are unlikely to be very useful to document changes in land use. In our paper, we invoke a very simple machine learning method to infer land use change based on k-means clustering of sequences of land use based on pixel level classifications based on MODIS land use product . We sampled roughly 800,000 randomly selected points across the Amazon and developed a pixel level panel for these points, exploring the pattern of land use. Over a five year period a sequence of land use could look like:
Forest – Forest  – Shrubland – Shrubland – Cropland
is indicative of permanent  land use change towards farmland, while a sequence such as
Forest – Shrubland  – Shrubland - Forest – Forest
may be indicative of temporary deforestation, followed by forest regrowth. The larger the state space (i.e. the larger the individual set of land use classes), the more difficult does it become to classify individual sequences of land use. For example with 10 different states, there are 10^5  possible combinations. This is where dimensionality reduction as carried out by k-means clustering can help, by clustering or grouping sequences that are similar based on some numeric features.
While in the end, we decided to use a very simplified state space with only three states: Forest, Cropland and Shrubland the method is nevertheless instructive and useful for simple applications like this.
The Features that we use are simple counts, such as the number of transitions to the state of being Forested or away from the state of being Forested (MODIS Land use category <=5), to the state of being Cropland (MODIS land use category 12/ 14) or the length that a pixel is classified as shrub land (in between cropland and forested). In addition, we count the length of repeat patterns, such as SCSC which may indicate crop rotation.
The separation achieved using R’s built in kmeans() function with different number of clusters with the different numeric features is illustrated below:

We can look at the individual clusters and then it is up to the researcher to decide upon how to interpret the resulting clusters. In our case, there was a clear separation into two clusters that indicate permanent deforestation as 100% of the sequences falling in that category had been classified as cropland at least once. There is an inbetween class, a class that indicates clearly temporary deforestation due to patterns of forest regrowth and a category that rests somewhere in between temporary and permanent.
Lastly, the big cluster consists of the bulk of pixels that are always forested.
Permanent vs Temporary and Forest Use
Our results , based on a simple difference in difference analysis as well as a matching difference in difference (as e.g. carried out by Chris Nolte and many others), suggests that pixels that become protected are more likely to remain in a forested state after a protected area is established.
In terms of permanent and temporary deforestation, our results suggest that – while permanent deforestation goes down, temporary land use patterns actually seem to become more likely. Â This could suggest that environmental protection may induce some behavioural changes at the margin, whereby settlers, rather than trying to develop legal claims over land actually just turn to extract the natural resources on the land and move on. Naturally, such behavior is much more difficult to prevent through policing and enforcement efforts.
References
Assunção, J., & Rocha, R. (2014). Getting Greener by Going Black : The Priority Municipalities in Brazil. Mimeo.
Hidalgo, F. D., Naidu, S., Nichter, S., & Richardson, N. (2010). Economic Determinants of Land Invasions. Review of Economics and Statistics, 92(3), 505–523. http://doi.org/10.1162/REST_a_00007
EspÃrito-Santo, F. D. B., Gloor, M., Keller, M., Malhi, Y., Saatchi, S., Nelson, B., … Phillips, O. L. (2014). Size and frequency of natural forest disturbances and the Amazon forest carbon balance. Nature Communications, 5, 3434. http://doi.org/10.1038/ncomms4434
Fetzer, T. R. (2014). Social Insurance and Conflict: Evidence from India. Mimeo.
Fetzer, T. R., & Marden, S. (2016). Take what you can: property rights, contestability and conflict.
Morton, D. C., DeFries, R. S., Shimabukuro, Y. E., Anderson, L. O., Arai, E., del Bon Espirito-Santo, F., … Morisette, J. (2006). Cropland expansion changes deforestation dynamics in the southern Brazilian Amazon. Proceedings of the National Academy of Sciences of the United States of America, 103(39), 14637–14641.